Números

Revisamos y profundizamos las ideas trabajadas en el primer trimestre:

Abajo, observamos una relación entre los números triangulares y los números cuadrados. ¿Puedes describirla con tus palabras?

Introducción a la trigonometría

El teorema de Pitágoras:

Una demostración visual del Teorema de Pitágoras: luego de reacomodar los 4 triángulos rectángulos iguales en blanco, el área en azul del cuadrado de la izquierda , a² + b², debe ser igual al área en rojo c² en el cuadrado de la derecha  

Por otra parte, trazando una paralela a un lado de un triángulo y "estirando" los otros dos, podemos observar que la suma de sus ángulos interiores es 180° :

Seguimos con la definición de la razones trigonométricas en un triángulo rectángulo:

Luego, definimos un ángulo orientado, compuesto por un lado fijo (semieje positivo de las x) y un lado móvil o terminal r

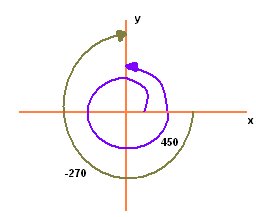
Vemos en la figura de abajo dos ángulos orientados: uno positivo y otro negativo:

Después definimos la funciones trigonométricas para un ángulo orientado:

y evaluamos sus signos según el cuadrante y valores para ángulos notables de 0 a 360°:

Pinchando en el punto C sobre la circunferencia y arrastrando, puedes observar como cambia el ángulo α  y la vez varían las coordenadas x e y, seno, coseno y tangente de α:




Tildando en la casilla correspondiente, se puede observar la representación cartesiana de la variación de las funciones seno, coseno y tangente de un ángulo orientado:

Medida de amplitud de ángulos: sistemas sexagesimal, centesimal y radial o circular. El radián

El sistema de medición de ángulos que conocemos desde los primeros años de la escuela primaria es el sistema sexagesimal, que consiste en dividir un giro o revolución en 360 partes iguales. Cada una de estas partes es 1 grado sexagesimal. En la figura, vemos un transportador con dos escalas. La interior corresponde al sistema centesimal, que divide a un recto en 100° centesimales, por lo cual una revolución equivale a 400° centesimales. En la exterior vemos los 360° sexagesimales que componen una revolución:

 y aquí un detalle de los 90° (sexagesimales) que componen un ángulo recto:

A su vez, un grado se puede dividir en 60 partes iguales. Cada una de estas partes es 1 minuto sexagesimal. Y éste, puede dividirse también en 60 partes iguales y cada una recibe el nombre de 1 segundo sexagesimal. Si todavía no te enteraste, sexagesimal viene de sesenta, y es el nombre que toma el sistema porque los submúltiplos del grado (el minuto y el segundo) se obtienen dividiendo por 60.

Resumiendo:

1 grado sexagesimal = 1°  

1 minuto sexagesimal = 1'

1 segundo sexagesimal = 1"

1 revolución = 360°

1 grado sexagesimal = 1° = 60' 

1 minuto sexagesimal = 60"

Hay otro sistema de medición de ángulos, usado internacionalmente, el sistema circular o radial, que describiremos a continuación. 
Si consideramos un segmento que gira, este segmento es el radio de una circunferencia (en un compás, el radio es el segmento imaginario entre el punto donde se pincha y el lápiz que marca la circunferencia). Cuando el radio r describe un cierto ángulo θ , subtiende ("encierra" o abarca) un arco de circunferencia s:

Ahora, centramos nuestra atención a calcular cuántas veces "entra" el radio r en el arco subtendido s. Esto es, la división entre s y r . Este resultado es la medida del ángulo θ en radianes

Un breve vídeo puede aclarar más la idea:

Aquí vemos un ángulo de 1 radian:

 y aquí uno de 2 radianes:

 y aquí 2, 3, 4, 5, 6 y, los 6,28... = 2π radianes que equivalen a una revolución o 360°:

Entonces, aquí tenemos una equivalencia fundamental entre los dos sistemas:

Variables. Expresiones algebraicas y monomios.

Ya hemos visto que en ciertas situaciones aparecen "cuentas" u operaciones en las cuáles hay números (cantidades constantes o "fijas", no cambian) y letras que representan a cantidades que cambian o varían, por lo cual reciben el nombre de variables.
En resumen, variables (letras) y constantes (números), conectados con operaciones: bienvenido al mundo de las expresiones algebraicas.

Notaciones de un número. Notación científica.

Hay diversas notaciones de un número (formas de anotarlo). Por ejemplo, la figura muestra un par de dados muy particulares:

De las distintas formas de escribir o anotar una cantidad, hay una que es de uso común por lo práctica para escribir números muy grandes o muy pequeños (haz un click en cada imagen para agrandarla y tómate el tiempo necesario para comprender los procedimientos mostrados)

Potencias de 10, factorización y notación científica.http://tube.geogebra.org/m/1554241
Posted by Matecontenidos on Miércoles, 2 de septiembre de 2015

Para practicar: Potencias de 10 y notación científica.

Fracciones, decimales y porcentajes

En esta entrada trataremos la representación de partes de un total o entero. Esta idea conduce a tres maneras  o formas de hacerlo y que, obviamente, son equivalentes entre si: fracciones, decimales y porcentajes

Más acerca de fracciones
Más acerca de decimales
Más acerca de porcentajes
Más acerca de fracciones, decimales y porcentajes
Para practicar más con fracciones, decimales y porcentajes, nivel de dificultad fácil
Para practicar más con fracciones, decimales y porcentajes, nivel de dificultad medio:

Las fracciones que tienen por denominador la unidad seguida de ceros son: . fracciones enteras . fracciones decimales . fracciones exactas Un porcentaje: . es un descuento. . es una fracción que tiene como denominador 100. . es un número decimal acabado en cero. En una tienda hay 500 yogures. El 60 % son de frutilla. ¿Cuántos yogures de frutilla hay en la tienda? . 300 . 450 . 360 De las siguientes, la fracción decimal es: . 12/106 . 348/100 . 7/15 En el colegio, de cada 100 alumnos, 15 juegan al ajedrez. ¿Cuántos alumnos juegan al ajedrez? . el 100 % de los alumnos. . el 15 % de los alumnos. . el 85 % de los alumnos. Un estacionamiento tiene 700 plazas. El 13 % de las plazas están ocupadas por motos y el 67 % por automóviles. ¿Cuántas plazas están sin ocupar? . 140 . 91 . 469 En la carrera de obstáculos, Montse llegó a la meta en 785 centésimas; Carlos en 6.785 milésimas y Álvaro en 79 décimas. ¿Quién corrió más rápido? . Montse . Carlos . Álvaro Si el 62 % de los 150 animales que ha atendido la veterinaria esta semana son perros, ¿cuántos perros ha atendido en total? . 93 . 87 . 62 En una encuesta hecha a 2.000 personas sobre su comida favorita, el 28 % ha elegido pastas, el 32 % carnes y el resto pizza. ¿Cuántas personas han elegido pizza? . 800 . 560 . 640 El 72 % de 3.500 es: . 3428 . 2520 . 3052

Examen electrónico de fracciones, decimales y porcentajes