"Aprender es buscar respuestas, pero para ello hacen falta las preguntas. ¿Quién se formula cuestiones matemáticas sobre lo que ve, hace, escucha o vive?. A mirar matemáticamente, a plantear problemas y a resolverlos también se aprende...Tal vez no se trate de un conocimiento novedoso a nivel mundial, pero habremos llevado a cabo un proceso prácticamente idéntico al del matemático profesional. Sin duda merecemos sentirnos tan dichosos como él. La experiencia educativa demuestra que así es..." Miquel Albertí Palmer
Los sábados por la mañana, en general, me acerco por la Feria Franca Municipal para conseguir frutas y verduras, buenas y baratas. Manzanas, melones y frutas secas de primera en el puesto número 3, "Las Negritas"; huevos frescos en el puesto 6, "Silvia".
En una oportunidad, no recuerdo bien para qué, compré un cartón de huevos. Como casi todos saben, el "cartón de huevos" es una plancha de 5 x 6 huecos que contiene 30 huevos, es decir, dos docenas y media.
Para variar, por h o por b, no puse manos a la obra a lo que tenía que hacer y el cartón con los 30 huevos quedó por ahí estorbando ese fin de semana. Pero, en los primeros días de la siguiente, hice una preparación y usé 4. Los elegí al azar y, curiosamente o casualmente, los restantes determinaron el siguiente arreglo o patrón:
La disposición anterior es simétrica respecto a un eje vertical (imaginario) que
pasa por el punto medio de los lados de medida 6 y divide al cartón en dos partes de 5 x 3, "una reflejo de la otra", si pensamos al eje de simetría como un espejo:
A estas disposiciones, arreglos o patrones simétricos determinados por la posición de los huevos en el cartón los llamaremos simetrías axiales (axial quiere decir relativas a un eje). Abajo va otra:
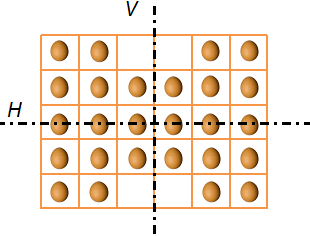
La cuestión se puede complejizar si tenemos en cuenta también el otro eje de simetría que tiene el cartón, el horizontal H:
Por ejemplo, la siguiente es una simetría axial doble con 26 huevos:
Es más, para huevear en profundidad, se pueden considerar tableros cuadrados que tienen 4 ejes de simetría, H, V, D1 (diagonal 1) y D2 (diagonal 2):
Para entretenerse. Eso si, sin romper los huevos.
